1. Navn
"Fibonaccis finurlige spiral"
2. Kort beskrivelse
Fibonaccis finurlige spiral
- om hvordan alt henger sammen med alt
NB! Til deg som vil prøve ut opplegget.
Det lønner seg nok å lese punkt 4.2 først – der står bakgrunnsinformasjonen til alt som beskrives i opplegget. I denne modulen skal elevene se sammenhenger i naturen. De skal få oppleve hvordan matematikken hjelper oss å beskrive hvordan naturen rundt oss er.
Eksempelvis:
Hva er sammenhengen mellom leddene i fingrene, kaninenes parringssyklus og Nidarosdomen?
3. Dagsplan
10.00: Oppmøte.
Opprop. Fortelle om hva dere skal finne ut av sammen i dag. Noen momenter her
er: Matematikk er et språk – det hjelper oss til å beskrive ting vi ikke klarer å beskrive
uten matematikk. For å illustrere hvor begrenset språket vårt er, pleier jeg å be elevene
fortelle hvordan de ville beskrive fargen blå for et menneske som aldri har sett.
Det er i beste fall svært vanskelig. Bruke dette som et eksempel på at hverdagsspråket
vårt har en del begrensninger – vi trenger ofte andre språkformer for å beskrive det
som er vanskelig å sette ord på. Følelser beskrives gjerne godt gjennom kunst; musikk,
dikt, bilder osv. En del problemer og hendelser og forløp beskrives godt gjennom for
eksempel matematikk.
Fortelle litt om Fibonacci og at han fant ut noe som en del mennesker mener er nøkkelen til universet!
10.20: Opplegget:
Beskriv Fibonaccis kaninproblem. Les opp premissene for kaninenes familieforøkning
som er beskrevet under punkt 4.2. Be elevene lage familietreet etter fem måneder.
De velger selv gjenstander fra naturen som representerer de forskjellige kaninene,
og legger dette under hverandre på bakken.
Etter at de har jobbet med dette en stund (det er ganske krevende og krever god
systematikk, så sett av litt godt med tid), så kan dere samles og se om dere klarer
å skrive ned tallrekka som kaninfamilien gir. Etter at dere har kommet fram til at den
er 1, 1, 2, 3, 5, så er neste oppgave å finne ut av hvor mange kaniner det blir fremover
etter de neste fem månedene, men det skal de finne ut av ved å tenke seg fram til
svaret, ikke ved å legge ned gjenstander. Her vil som oftest noen ganske fort se at
de må legge sammen to og to tall for å finne det neste.
11.00: Elevene forsyner seg med en neve fyrstikker,
- og får nå beskjed om at de skal bruke dem til å lage kvadrater som følger tallrekka.
Kvadratene skal henge sammen, slik at de bygger på hverandre (se instruksjon under
4.2). Hvis dere vil, kan dere lime dem fast på papplater, men det er ikke nødvendig…
Etter at kvadratene er lagt, forsyner elevene seg med et godt stykke tråd.
Den legger de fra hjørne til hjørne i kvadratene, slik at dere får opp Fiboanccis spiral.
Vis bilder av former i naturen som har den spriralen. Hvis dere er ved et sted der
dere kan finne sneglehus, så sendes elevene ut på jakt etter det. Ta dem med
tilbake til campen, og sammenlikn husets form med spiralene dere har laget.
11.30: Elevene skal nå regne litt.
De deler to tall et stykke ute i tallrekka på hverandre (89/55 funker best), og får da
svaret 1,618. Spør om noen vet hva det tallet er. Hvis ingen vet, forteller du om
det gylne snitt, og at det er et tallforhold som vi finner svært mange steder.
Som en start kan dere se etter det gylne snitt på kroppen. Gi elevene målebånd,
og la dem se om de finner det gylne snitt ut fra de forholdene som er beskrevet
under 4.2 De deler da det største tallet på det minste, og ender forhåpentligvis
opp rundt 1,6
12.00-12.30: Lunsj
12.30: Nå skal elevene finne den gylne vinkel.
La dem dele 360° på 1,618, og finne ut at den gylne vinkel er 222,5° eller 137,5°.
Fortell om hvordan noen blader fordeler seg på denne måten, og hvordan frøene
fordeler seg i noen planter. La dem prøve å se og tegne opp hvordan frøene ville
fordele seg hvis de la seg 90° på hverandre, eller for eksempel 30° på hverandre.
Til dette trenger de en gradskive. Etterpå kan de prøve å fordele frøene med 222,5°.
Dette er vanskelig. Belag deg på å måtte hjelpe til. En måte å avhjelpe litt, er hvis
du lar dem tegne opp mange sirkler utenpå hverandre, med for eksempel 5mm
avstand mellom hver. Når de har fylt opp så mange frø det er plass til på en sirkel
(altså så mange som gradene tillater at det blir (med 90° vil du se at det bare er
plass til fire på hver sirkel)), så går de ut til neste sirkel, og fortsetter.
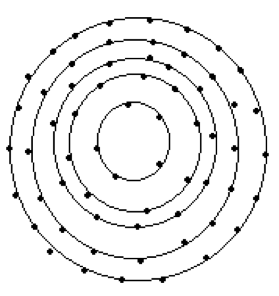
Gjennom dette arbeidet vil de se at det er mye mer økonomisk å pakke frøene etter
den gylne vinkel, enn etter andre vinkler. Har du med deg en solsikke, er dette
tidspunktet å vise den på.
13.15: Finne Fibonaccitall i naturen.
La elevene finne noen store furukongler. La dem forsyne seg med to tusjer med
forskjellige farger. Forklar hvordan konglene er laget (med spiraler som går til
høyre og venstre), og la elevene markere hvor mange spiraler som går til venstre
og hvor mange som går til høyre. Etter å ha telt opp vil dere se at det er to nabotall
i Fibonaccispiralen.
Har du med en ananas, så er det på tide å se på den nå. Hvis noen har med seg
et eple, kan dere se om dere finner ut at det er fem frørom inne i det – altså et
Fibonaccitall. Nå skal elevene ut på jakt etter Fibonaccitall i naturen!
14.00 eller senere alt ettersom hvor engasjerte elevene er…
På nettet finnes det flere bilder av både Nidarosdomen og Pantheon. Vis elevene
hvordan det gylne snitt ser ut i et rektangel, altså at en side er 1,6 ganger så lang
som en annen. La dem måle opp og sjekke ut bankkort og iPhoner, og se om de
er laget etter det gylne snitt. Etterpå kan de få bilder av Pantheon, Nidarosdomen
eller andre bygg du vet om, og finne det gylne snitt på dem. I komplekse bygg,
må man gjerne dele opp bygget i forskjellige deler – ta øverste rekke av vinduer
til taket, eller et annet tydelig skille i bygget.
.
4. Faglige innholdsmomenter
4.1 Faglig tema
• Hva er sammenhengen mellom leddene i fingrene, kaninenes parringssyklus og Nidarosdomen?
• Hvordan systematisere og beskrive et hendelsesforløp som gjentar seg på en bestemt måte?
• Gå fra en fysisk modell til å beskrive modellen med tall
• Gjenskape Fibonaccis tallrekke
• Kunne gjøre om tallrekka til Fibonaccis spiral
• Se sammenhengen mellom tallrekka og det gylne snitt
• Kunne finne den gylne vinkel
• Gjennom den gylne vinkel kunne tegne opp hvordan en del planter fordeler
frøene sine, hvordan en del planter fordeler bladene sine og hvordan konglene fordeler skjellene sine
• Finne eksempler på gjenstander i naturen som kan kobles til Fibonaccis tallrekke
• Finne det gylne snitt i kroppen
• Finne det gylne snitt i arkitektur (blant annet Nidarosdomen)
Aktiviteter:
- Sette opp Fibonaccis problem med gjenstander man finner i naturen
- Legge opp kvadrater til Fibonaccis spiral, forme spiralen med tråd
- Finne planter som har med Fibonccitallene og spiralen å gjøre
- Måle og finne det gylne snitt i kroppen og i arkitektur
_________________________________________________
Matematikk:
Lære om det gylne snitt og om den gylne vinkel.
Bruke gradskive.
Måle med målebånd.
Lære hva forhold er. Regne ut forhold.
Bruke matematikkspråket, og erfare at vi gjennom matematikk kan forklare
og sette ord på ting og sammenhenger som er nærmest umulig å forklare
uten matematikk.
Naturfag:
Se at mye i naturen kan beskrives med det gylne snitt.
Se nærmere på detaljer i gjenstander i naturen – oppleve
naturen på en annen måte enn de kanskje er vant til.
Oppleve at en enkel tallinje er utgangspunktet for en forklaringsmodell for
svært mye av det vi ser rundt oss, både i naturen, men også menneskeskapt.
Historie:
Lære om Fibonacci, en av Europas største matematikere fra middelalderen.
Lære at det ikke alltid er store og vanskelige formler og utregninger som
ligger til grunn for mange av de store oppdagelsene mennesket har gjort.
Forskning og hypoteser kan ofte ha et enkelt utgangspunkt.
4.2 Faglig bakgrunnsinformasjon -for aktiviteten(e) og åpne spørsmål
Leonardo Fibonacci var en italiensk matematiker som levde på 1200-tallet.
Det er ikke han som oppfant Fibonaccis tallrekke, det var det inderne som
gjorde, men det var han som gjorde den kjent i vesten. Fibonacci har også
æren for at vi begynte med dagens tallsystem, titallssystemet, da det var han
som innførte det også til Europa. Før det brukte vi romertall. Hans mest
berømte bok, der både titallssystemet og tallrekken forklars, heter "Liber Abaci".
Fibonaccis kaniner:
Det sies at det hele startet med at Fibonacci satte opp et problem. Han så for
seg at to kaniner møttes som barn. Etter en måned ble kaninene kjønnsmodne
og parret seg. Kaninmoren gikk en måned drektig før hun fødte, og da fødte
hun to nye kaniner.
Disse to nye kaninene ble også en måned gamle før de ble kjønnsmodne.
Etter det parret de seg også. Mora går en måned drektig, så føder hun et nytt
kaninpar, og familieforøkelsen fortsetter på samme måte videre.
Samtidig med at de neste parene kommer til, blir kjønnsmodne, parrer seg
og går en måned gravid, så fortsetter de eldre parene å parre seg, og føde
nye unger hver måned.
Fibonacci jobbet med å sette opp et slektstre for denne kaninfamilien.
Han satte som premiss at alle mødrene kun fødte to nye unger, at disse
ungene siden ble kjærester, og at de fortsatte å føde nye unger hver
måned etter at de ble kjønnsmodne. Familietreet ble seende slik ut:
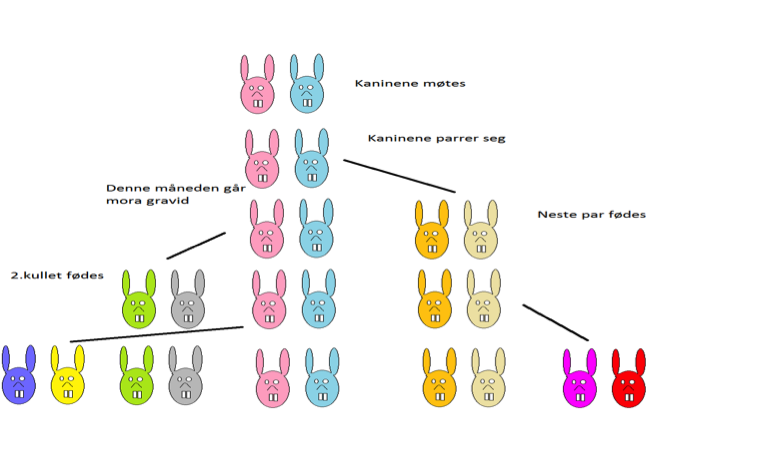
Først var det ett par, neste måned var det også ett par. Etter det er det to par tilstede.
Etter det tre par osv. Hvis man setter opp denne tallrekka, så får man
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… og dette er den berømte tallrekka til Fibonacci.
Den kan brukes til mye forskjellig.
Hvis du ser på pekefingeren din (eller de andre fingrene, bortsett fra tommelen),
så ser du at den er satt sammen av tre ledd. Hvis du måler og legger sammen
lengden av de to første leddene, så er de like lange som det tredje leddet (det
tredje leddet går til knoken din). Sammenhengen mellom leddene blir altså 1, 1, 2.
Denne oppbyggingsmåten ser vi også andre steder i naturen.
Tallrekka kan enten lages ved at man finner ut hvor mange kaniner som kommer
til verden, men man kan også finne ut av den ved å regne ut de neste leddene.
Sammenhengen i tallrekka er nemlig at man legger sammen to og to sifre.
1+1 = 2, 1+2=3, 3+2= 5, 5+3= 8 osv.
Den andre sammenhengen som gjør tallrekka spesiell, er at hvis du deler et
tall på tallet foran, så får du tilnærmet tallet 1,6 – det gylne snitt. Dette fungerer
ikke på de tre første tallene, de blir for unøyaktige, men etter tallet 3, så fungerer
det bedre og bedre.
Det gylne snitt er et forholdstall som dukker opp svært mange steder rundt oss.
Kroppen vår har mange gylne snitt i seg:
Kroppen og det gylne snitt:
Kroppen vår er 1,6 ganger høyden fra navlen til bakken.
Avstanden fra skulderen til fingertuppen, og fra albuen til fingertuppen.
Avstanden fra albuen ut til fingertuppen, og fra håndleddet ut til fingertuppen.
Avstanden fra skulderen opp til toppen av hodet, og hodets høyde.
Fra navlen opp til toppen av hodet, mot skuldrene opp til toppen av hodet.
Det gylne snitt andre steder:
I tillegg til kroppen, har vi mennesker også laget mye som følger det gylne snitt.
Veldig mange bygg har gylne snitt i seg, og mange av de klassiske byggverken
har det. Bankkortene våre og iPhonen følger også det gylne snitt. Man har også
funnet flere bygg som har hatt det gylne snitt i seg lenge før matematikerne hadde
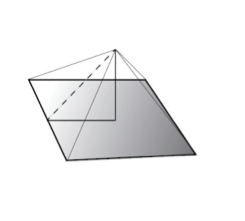
begynt å beskrive det gylne snitt. Kheopspyramiden er ett eksempel. Høyden i
pyramiden er 147 meter. Den skrå utsiden er 186,9 meter (hypotenusen), og
kateten langs bakken inn til midten, er 115,5 meter. Hvis du deler hypotenusen
på bakkekateten får du det gylne snitt.
Nidarosdomen har også mange gylne snitt i utformingen sin. Pantheon i Hellas er et
annet eksempel, der det gylne snitt er brukt nesten helt konsekvent. Mange mener at
mennesket liker å se på ting som har det gylne snitt i seg.
Det gylne snitt i naturen/ den gylne vinkel:
I naturen ser vi også mange eksempler der det gylne snitt dukker opp. For å se det
trenger vi å kjenne til "den gylne vinkel". Den gylne vinkel finner vi ved å ta 360° og
dele på 1,618. Da får vi at den gylne vinkel er 222,5° eller 137,5°.
Mange planter fordeler bladene sine etter den gylne vinkel. Hvis vi tenker oss at
bladene hadde vokst ut ett og ett, så ville først et blad kommet ut. Det neste bladet
ville da komme ut 222,5° etter det, det neste 222,5° etter det osv. Da ville fordelingen
kunne se slik ut:
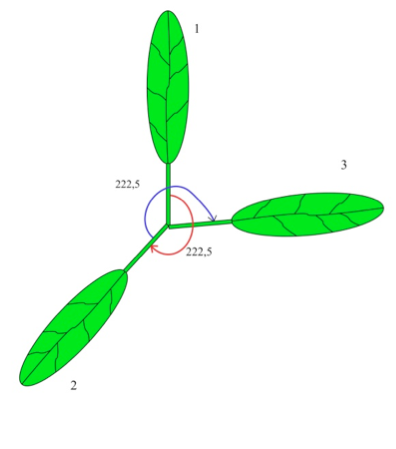
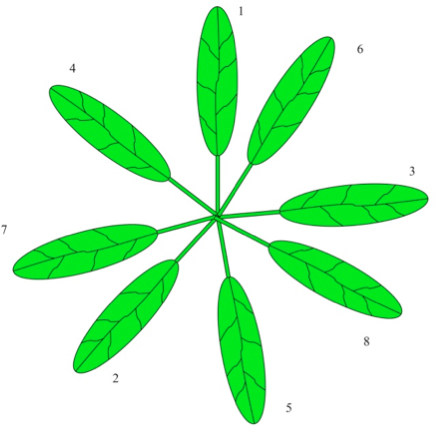
Ved å fordele seg etter den gylne vinkel, vil ikke bladene skygge for hverandre og
ta inn maksimalt med sollys, og de vil kunne samle mer vann ned til røttene.
Det er ikke bare bladene som fordeler seg etter den gylne vinkel. Flere blomster pakker
frøene sine etter den gylne vinkel også. Solsikken er kanskje den blomsten der det er
lettest å få øye på. Fordelingen av frø følger samme prinsipp som fordelingen av blader,
og fordelingen ser da sånn ut:

Dette er den mest effektive måten å pakke på, slik at det blir plass til mest mulig frø på
liten plass. For å se et eksempel som er svært lite økonomisk, kan man prøve å "skyte
ut" frø med 90° mellom hvert frø. Det ville da sett slik ut:
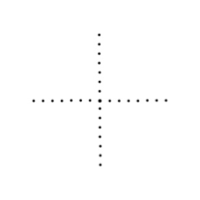 Fibonaccitall i ananaser og kongler:
Fibonaccitall i ananaser og kongler:
En litt særere side av Fibonacci og naturen, er at mange planter har Fibonaccitallene
representert i hvor mange frø de har. Åpne et eple og se hvor mange frørom du finner.
Frøhuset har fem rom, fem er et tall i tallrekka til Fibonacci. Tell kronbladene på en
prestekrage, antall blad er som oftest 13, 21 eller 34. Tilfeldig? Neppe – ifølge
Fibonaccientusiaster!
Men det er ikke bare slik at Fibonaccitallene opptrer alene i frøhus og planter, det er
også flere planter som har Fibonaccitallene i kombinasjon. Hvis du ser på utsiden av
en ananas, så er den satt sammen av mange sekskanter. Sekskantene ligger etter
hverandre i spiraler (du kan starte på bunnen og følge "rekkene" av sekskanter etter
hverandre, og du vil se at de går som spiraler oppover ananasen). Disse spiralene
går både mot høyre og venstre. Siden hvert skjell på ananasen har seks kanter, kan
du velge om spiralen du skal følge skal gå slakt oppover, eller om det skal være en
spiral som går brattere oppover. Hvis du teller antall spiraler som går slakt, vil du
finne ut at antallet spiraler er et Fibonaccitall. Teller du antallet spiraler som går bratt,
så finner du at det også er et Fibonaccitall. Se på tegningen under:

Hvis du finner en furukongle, så er den også satt sammen av små skall.
Titter du på bunnen, ser du at konglen også går utover i spiraler som kan
gå både mot høyre og venstre. Teller du antall spiraler, vil du finne at antall
spiraler som går mot venstre og antall spiraler som går mot høyre er begge
Fibonaccitall, OG de er to nabotall i tallrekka, for eksempel 8 og 13.
 Fibonaccis spiral:
Fibonaccis spiral:
Den siste siden av Fibonacci som hører med til dette opplegget, er Fibonaccis spiral.
Tallrekka husker vi var 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
Hvis du nå lager kvadrater av disse tallene, så får du en bestemt figur. Du begynner
med å lage et kvadrat med sidelengde 1. Ved siden av dette kvadratet lager du et til
med sidelengde 1(1, 1…) Neste kvadrat skal nå ha sidelengde 2. Veggene til dette
kvadratet passer nå veldig fint å legge over eller under de to første kvadratene, da
de to første til sammen har lengde 2.
Jeg velger å legge mitt kvadrat på undersiden av de to første, slik:
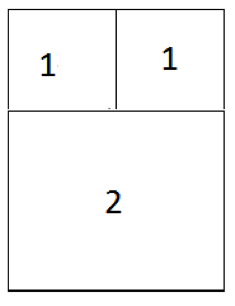
Det tredje kvadratet har sidelengde 3, og får naturlig plass på venstre side.
5 får plass på toppen, 8 til høyre osv. Man kan bygge på så mange kvadrater
man gidder eller får plass til.
Når det er gjort, så står du igjen med kvadrater som for eksempel ligger slik:
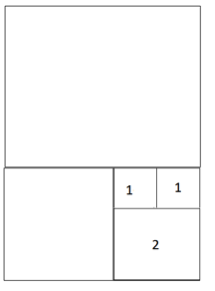
Magien skjer når du trekker kvarte halvsirkler som buede diagonaler gjennom
kvadratene. Du begynner nede i venstre hjørne i det første venstre kvadratet,
trekker buen gjennom hele kvadratet, over i detneste, gjennomdet og over i det
neste osv. Da ser det etter hvert slik ut:
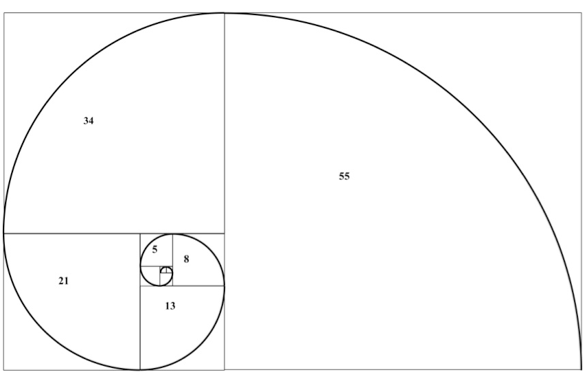
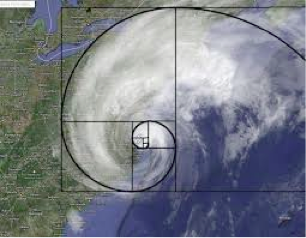
Denne spiralen ser vi mange steder i naturen. Sneglehusene har formen,
sjøhestenes hale har den, galaksene har den, støttennene til elefantene har
samme bue som ytterste del, det samme har øret ditt. En del bregner krøller
seg sammen på tuppen som denne spiralen. Noen mener store bølger har
denne formen rett før de knekker over.




 Kommentar:
Kommentar:
Fibonaccis tallrekke har blitt tatt til inntekt for mye rart. Det er flere forskere som
mener at tallrekka med sin tilhørende spiral har blitt tatt til inntekt for å forklare
mer enn den kan. Blant annet er det noen som mener at spiralen ikke er en god
modell for sneglehusene, og at det finnes andre og bedre spiraler som modeller.
Med hensyn til grunnskolematematikk og hvor målet er å vise elevene at
matematikk kan forklare mye som verbalspråket vårt ikke kan, så synes ikke jeg
det gjør noe om spiralen ikke er en helt korrekt modell for spiralene vi finner i
naturen. For noen har sammenhengene Fibonacci beskriver blitt brukt som et
gudsbevis – at denne enkle tallrekka er "koden" som en verdensskaper har
benyttet seg av for å skape verden. Gud vet…
5. Egnet sted for gjennomføring
Dette opplegget krever ikke noen spesiell plass, men hvis man skal finne planter og sneglehus som har tilknytning til Fibonacci, så er et sted med furukongler, forskjellige blomster og tilgang på sneglehus vesentlig.
6. Anbefalt aldersgruppe
Dette opplegget fungerer for de fleste aldersgrupper, alt ettersom hvor langt man vil trekke det. Det har fungert fint for barnehagebarn til videregående elever.
7. Anbefalt antall deltakere pr leder
Det kan bli mange spørsmål, så optimalt er det ikke flere enn 15 pr. leder, men hvis du har god oversikt, går det fint med flere - elevene bør jobbe sammen to og to eller tre og tre.
8. Utstyr og materiell
8.1 Utstyr
Pose med fyrstikker uten hode (fås på hobbybutikk)
Garnnøste eller hyssing
Målebånd eller tommestokk
Tusjer i to forskjellige farger til alle lag
Blyanter og skrivepapir
Gradskive
Passere
Bilder av støttenner, store bølger, halen til en sjøhest, bregne som krøller seg, galakse. Bildene bør nok være laminert.
Eventuelt:
Papplater og lim til å lime fast fyrstikkene når elevene legger opp Fibonaccispiralen
En eller flere ananaser til å forske på
Solsikke å forske på
Hvis dere er et sted uten furukongler, kan det være greit å ta med det.
Bilder av Pantheon eller andre bygg med det gylne snitt i seg.
8.2 Materiell
Print gjerne ut bilder som ligger i faglig innhold og laminer disse - eventuelt legg dem inn i en presentasjon slik at de kan benyttes i fagintro.
9. Praktisk informasjon
9.1 Oppmøtetid og -sted
Avgjøres av hver enkelt camp
9.2 Hentetid og -sted
Avgjøres av hver enkelt camp
9.3 Utstyr for deltakere
9.3.1 Fast utstyr som må være med deltagerne hver dag:
Avgjøres av hver enkelt camp
9.3.2 Utstyr for denne modulen:
Avgjøres av hver enkelt camp
10. Sikkerhet
10.1 Krav til veiledere
Opplegget stiller ingen krav til sikkerhet, bortsett fra hvis dere er i nærheten av sjø for å finne sneglehus.
10.2 Krav til aktiviteten
Ingen spesielle krav, - se generelle krav om sikkerhet her
http://www.newtoncamp.no/intranett.aspx
10.3 Ansvar og forsikring
Les generell informasjon om ansvar og forsikring her
http://www.newtoncamp.no/intranett.aspx
11. Utviklet av
Håvard Tjora på oppdrag fra Tekna